A Note of Caution

Everything we've computed so far looks pretty reasonable. However, lest you get the idea that finite difference schemes always work, let's try using (5) with grid sizes that do not satisfy the condition (6). For example, let's try to reproduce Figure 3 using $\delta x=0.01$ and $\delta t=0.0005$. This gives the following results:

Figure 10: Numerical solution of the diffusion equation for $\delta x=0.01$ and $\delta t=0.0005$, grid sizes which do not satisfy equation (6).

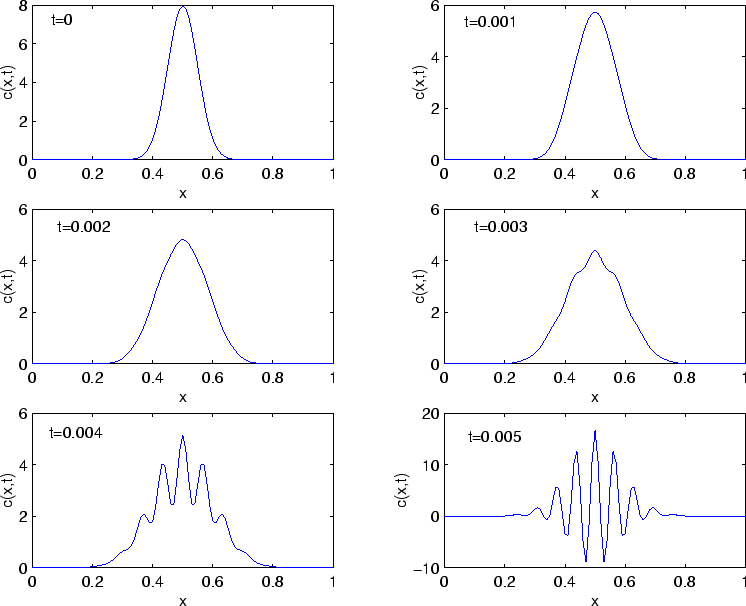We see that our numerical solution is not behaving in a reasonable way. In fact, if we integrate for longer times we find that the spurious oscillations for this numerical solution blow up to extremely large amplitude. The moral of this story is that you have to be careful when using finite differences to solve PDEs.