Solution of the Diffusion Equation by Finite Differences

The basic idea of the finite differences method of solving PDEs is to replace spatial and time derivatives by suitable approximations, then to numerically solve the resulting difference equations. Specifically, instead of solving for $c(x,t)$ with $x$ and $t$ continuous, we solve for $c_{i,j} \equiv c(x_i,t_j)$, where

$$x_i \equiv i \delta x,$$

$$t_j \equiv j \delta t$$

define the grid shown in Figure 1.

Figure 1: Grid for our finite difference approximations. The point labelled $i,j$ corresponds to $(x,t) = (x_i,t_j)$, etc.

Derivatives of $c$ are approximated in terms of the values of $c$ at grid points. For example, we know that

$$\frac{\partial c}{\partial x} = \lim_{\Delta x \rightarrow 0} \frac{\Delta c}{\Delta x}.$$

This derivative evaluated at the grid point $(x,t) = (x_i,t_j)$ can be approximated in many different ways, the simplest being the following:

• Forward Difference:
  
  $$\left. \frac{\partial c}{\partial x} \right\vert _{x_i,t_j} ... ..._{i,j}}{x_{i+1} - x_i} = \frac{c_{i+1,j} - c_{i,j}}{\delta x},$$
  
  

• Backward Difference:
  
  $$\left. \frac{\partial c}{\partial x} \right\vert _{x_i,t_j} ... ...i-1,j}}{x_i - x_{i-1}} = \frac{c_{i,j} - c_{i-1,j}}{\delta x},$$
  
  

• Central Difference:
  
  $$\left. \frac{\partial c}{\partial x} \right\vert _{x_i,t_j} ... ...x_{i+1} - x_{i-1}} = \frac{c_{i+1,j} - c_{i-1,j}}{2 \delta x}.$$
  
  

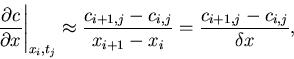
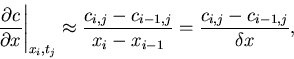
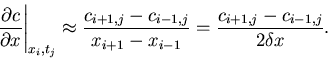
The second derivative at the grid point $(x_i,t_j)$ may be approximated by using

$$\frac{\partial^2 c}{\partial x^2} = \lim_{\Delta x \rightarr... ...\Delta \left(\frac{\partial c}{\partial x} \right)}{\Delta x}.$$

Instead of using approximations for $\frac{\partial c}{\partial x}$ in terms of the values of $c$ at $x_{i+1}, x_i$ as for the forward difference, or at the points $x_i, x_{i-1}$ as for the backward difference, let's imagine instead that we evaluate it at the (fictitious) points $x_{i+\frac{1}{2}}, x_{i-\frac{1}{2}}$, defined in the obvious way. Then, using central difference approximations for the spatial derivatives evaluated at these points,

$$\left. \frac{\partial c}{\partial x} \right\vert _{x_{i+\fra... ... c_{i,j}}{x_{i+1}-x_i} = \frac{c_{i+1,j} - c_{i,j}}{\delta x},$$

$$\left. \frac{\partial c}{\partial x} \right\vert _{x_{i-\fra... ..._{i-1,j}}{x_i-x_{i-1}} = \frac{c_{i,j} - c_{i-1,j}}{\delta x}.$$

Then

$$\left. \frac{\partial^2 c}{\partial x^2} \right\vert _{x_i} \approx \frac{\left. \frac{\partial c}{\partial x} \right\vert _{x_{i+\fr... ...ial x} \right\vert _{x_{i-\frac{1}{2}}}}{x_{i+\frac{1}{2}} - x_{i-\frac{1}{2}}}$$

$$= \frac{c_{i+1,j} - 2 c_{i,j} + c_{i-1,j}}{(\delta x)^2}.$$ (3)

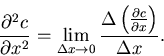
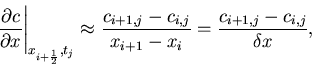
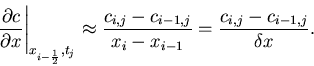
We can approximate derivatives with respect to time in the same way. For example, the forward difference approximation for $\partial c/\partial t$ at the grid point $(x_i,t_j)$ is

$$\left. \frac{\partial c}{\partial t} \right\vert _{x_i,t_j} ... ..._{i,j}}{t_{j+1} - t_j} = \frac{c_{i,j+1} - c_{i,j}}{\delta t}.$$ (4)

It should be noted that these finite difference approximations are only valid to some order in $\delta x$ or $\delta t$. The error in the approximations is called the truncation error. It is possible to get approximations which are valid to higher order by using more grid points in the approximations. This is all quite important, but for our purposes the approximations given above will be sufficient.

Using the approximations (3) and (4) in (2), and rearranging, we get the following difference equation which can be iterated to find the approximate solution to equation (2):

$$c_{i,j+1} = c_{i,j} + \frac{\delta t}{(\delta x)^2} (c_{i+1,j} - 2 c_{i,j} + c_{i-1,j}).$$ (5)

This is called an explicit numerical scheme because the computation of $c$ at $t_{j+1}$ is completely determined by our computation of $c$ at $t_j$. This scheme is also called consistent because the finite difference approximations have a truncation error that approaches zero in the limit that $\delta t \rightarrow 0$, $\delta x \rightarrow 0$.

Although this is a consistent method, we are still not guaranteed that iterating equation (5) will give a good approximation to the true solution of the diffusion equation (2). A numerical scheme is called convergent if the solution of the discretized equations (here, the solution of (5)) approaches the exact solution (here, the solution of (2)) in the limit that $\delta t \rightarrow 0$, $\delta x \rightarrow 0$.

For linear equations such as the diffusion equation, the issue of convergence is intimately related to the issue of stability of the numerical scheme (a scheme is called stable if it does not magnify errors that arise in the course of the calculation). Indeed, the Lax Equivalence Theorem says that for a properly posed initial value problem for a linear PDE, and a consistent finite difference approximation, stability is the necessary and sufficient condition for convergence. Moreover, it can be shown that the scheme given by (5) is only convergent when

$$\frac{\delta t}{(\delta x)^2} \le \frac{1}{2}.$$ (6)

These issues are also quite important, but this is not the appropriate place to go into them in more detail. All of the details are described, for example, in A First Course in Numerical Analysis of Differential Equations by Arieh Iserles, Cambridge University Press, 1996.

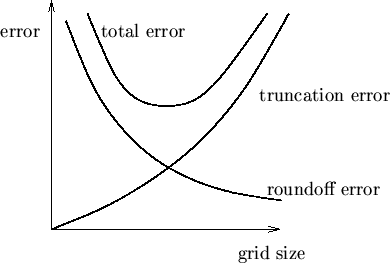
However, before moving on, let me emphasize that as the sizes $\delta t$ and $\delta x$ are made smaller, the truncation error of approximating the partial derivatives by finite differences decreases. However, for smaller sizes, more computations need to be done to get solutions for the same domain and total time, which leads to increased roundoff error. The total error as a function of these sizes is sketched in Figure 2.

Figure 2: Sketch of errors as functions of the grid size for a finite difference calculation. Here it is assumed that the solution is calculated on the same domain and for the same total time.