


Next: An SEIR model with
Up: APC/EEB/MOL 514 Tutorial 4:
Previous: An SIS model with
We'll now consider the epidemic model from ``Seasonality and
period-doubling bifurcations in an epidemic model'' by J.L. Aron and
I.B. Schwartz, J. Theor. Biol. 110:665-679, 1984 in which
the population consists of four groups:
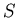 is the fraction of susceptible individuals (those able to contract the disease),
is the fraction of susceptible individuals (those able to contract the disease),
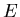 is the fraction of exposed individuals (those who have been infected but are not yet infectious),
is the fraction of exposed individuals (those who have been infected but are not yet infectious),
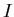 is the fraction of infective individuals (those capable of transmitting the disease),
is the fraction of infective individuals (those capable of transmitting the disease),
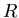 is the fraction of recovered individuals (those who have become immune).
is the fraction of recovered individuals (those who have become immune).
Note that the variables give the fraction of individuals - that is,
we have normalized them so that
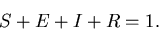 |
(9) |
Furthermore, suppose that
- There are equal birth and death rates
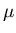 ,
,
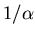 is the mean latent period for the disease,
is the mean latent period for the disease,
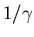 is the mean infectious period,
is the mean infectious period,
- recovered individuals are permanently immune,
- the contact rate
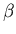 may be a function of time.
may be a function of time.
This leads us to consider the following model:
The variable 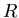 is determined from the other variables according to
equation (9).
When
is determined from the other variables according to
equation (9).
When
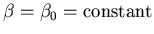 , this is a three-dimensional
autonomous system of ordinary differential equations, and is well
understood. Defining
, this is a three-dimensional
autonomous system of ordinary differential equations, and is well
understood. Defining
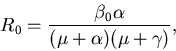 |
(13) |
it can be shown that for 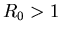 the model has a fixed point with
the model has a fixed point with 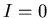 which
is unstable, and a fixed point with
which
is unstable, and a fixed point with 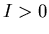 which is stable, etc. See Aron
and Schwartz for more detail and references.
which is stable, etc. See Aron
and Schwartz for more detail and references.
If 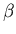 depends on time, we have a three-dimensional nonautonomous system,
which can be converted to a four-dimensional autonomous system as was
done above for the SIS model.
depends on time, we have a three-dimensional nonautonomous system,
which can be converted to a four-dimensional autonomous system as was
done above for the SIS model.



Next: An SEIR model with
Up: APC/EEB/MOL 514 Tutorial 4:
Previous: An SIS model with
Jeffrey M. Moehlis
2002-10-14
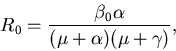
![]() depends on time, we have a three-dimensional nonautonomous system,
which can be converted to a four-dimensional autonomous system as was
done above for the SIS model.
depends on time, we have a three-dimensional nonautonomous system,
which can be converted to a four-dimensional autonomous system as was
done above for the SIS model.