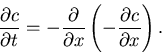Next: Numerical Solution of the
Up: APC591 Tutorial 5: Numerical
Previous: Solution of the Diffusion
Let's consider the diffusion equation with boundary conditions
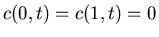 , that is, the concentration at the boundaries is
held at zero. Physically, this could correspond to our system being
in contact at its boundaries with a very large reservoir containing a very
small concentration of the chemical. Indeed, imagine that the reservoir is
so large that, even when some of our chemical escapes into it, the
concentration within the reservoir stays approximately equal to zero.
We enforce these boundary conditions in our finite difference scheme by
explicitly requiring that
, that is, the concentration at the boundaries is
held at zero. Physically, this could correspond to our system being
in contact at its boundaries with a very large reservoir containing a very
small concentration of the chemical. Indeed, imagine that the reservoir is
so large that, even when some of our chemical escapes into it, the
concentration within the reservoir stays approximately equal to zero.
We enforce these boundary conditions in our finite difference scheme by
explicitly requiring that
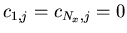 for all
for all 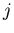 .
.
Before giving the Matlab code to numerically solve the diffusion equation,
let's rewrite this equation (2) as
We identify the quantity inside the parentheses as the flux 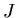 :
:
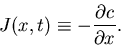 |
(7) |
Since this is a one-dimensional problem, the flux 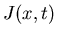 is the number of
particles
per unit time crossing
is the number of
particles
per unit time crossing 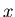 at time
at time 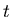 . A positive flux corresponds to
a net flow in the
. A positive flux corresponds to
a net flow in the 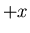 -direction, while a negative flux corresponds to a
net flow in the
-direction, while a negative flux corresponds to a
net flow in the 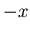 -direction. Because it's instructive, let's keep track
of the total number of particles which have crossed the boundaries at
-direction. Because it's instructive, let's keep track
of the total number of particles which have crossed the boundaries at 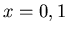 .
At
.
At 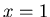 , this is
, this is
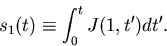 |
(8) |
At 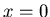 , we need to take into account the fact that a negative flux means
that a positive number of particles are leaving the domain. Thus, the
total number of particles which have crossed the boundary at
, we need to take into account the fact that a negative flux means
that a positive number of particles are leaving the domain. Thus, the
total number of particles which have crossed the boundary at 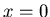 is
is
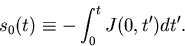 |
(9) |
The total number of particles within the box is given by
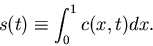 |
(10) |
By conservation of mass, it is expected that
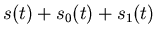 should
be a constant.
should
be a constant.
For definiteness, we'll consider the initial condition
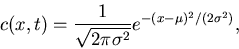 |
(11) |
i.e., a Gaussian with mean 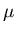 and variance
and variance 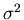 . This has been
normalized so that
. This has been
normalized so that
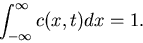 |
(12) |
We'll choose this Gaussian to be narrow enough that the initial condition
satisfies the boundary conditions at 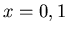 for all practical purposes,
so that
for all practical purposes,
so that



Next: Numerical Solution of the
Up: APC591 Tutorial 5: Numerical
Previous: Solution of the Diffusion
Jeffrey M. Moehlis
2001-10-24
![]() , that is, the concentration at the boundaries is
held at zero. Physically, this could correspond to our system being
in contact at its boundaries with a very large reservoir containing a very
small concentration of the chemical. Indeed, imagine that the reservoir is
so large that, even when some of our chemical escapes into it, the
concentration within the reservoir stays approximately equal to zero.
We enforce these boundary conditions in our finite difference scheme by
explicitly requiring that
, that is, the concentration at the boundaries is
held at zero. Physically, this could correspond to our system being
in contact at its boundaries with a very large reservoir containing a very
small concentration of the chemical. Indeed, imagine that the reservoir is
so large that, even when some of our chemical escapes into it, the
concentration within the reservoir stays approximately equal to zero.
We enforce these boundary conditions in our finite difference scheme by
explicitly requiring that
![]() for all
for all ![]() .
.