


Next: About this document ...
Up: APC591 Tutorial 4: From
Previous: Reduction to a Two-Dimensional
As for the FitzHugh's simplification of the Hodgkin/Huxley equations,
let's plot the nullclines for the two-dimensional system
(7,8). This is done in Matlab with the following
programs. First nullclines.m:
global nu sigma k kt L q h g
nu = 0.1;
%nu = 0.04;
sigma = 1.2;
k = 0.4;
kt = 0.4;
L = 10^6;
q = 100;
h = 10;
for i=1:250
g = 0.1*i;
gamma(i) = g;
null_alpha(i) = fzero('rhs_alpha',70);
null_gamma(i) = fzero('rhs_gamma',80);
end
figure(2)
hold on;
plot(gamma,null_alpha,'b');
plot(gamma,null_gamma,'r');
axis([0 25 40 100]);
xlabel('\gamma');
ylabel('\alpha');
Text version of this program
Next, rhs_alpha.m:
function r = rhs_alpha(alpha)
global nu sigma k L q h g
r = nu - sigma*phi(alpha,g);
Text version of this program
Finally, rhs_gamma.m:
function r = rhs_gamma(alpha)
global nu sigma k L q h g
lambda = q*sigma/h;
r = lambda*phi(alpha,g) - k*g;
Text version of this program
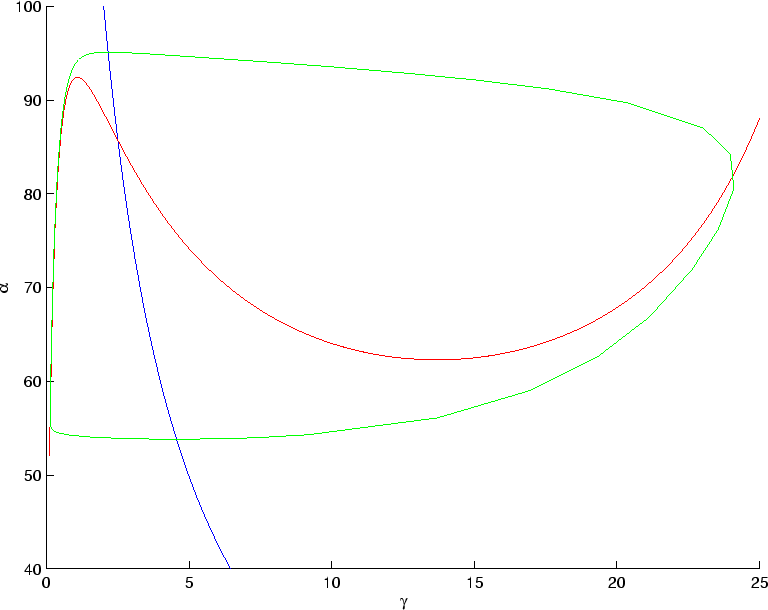
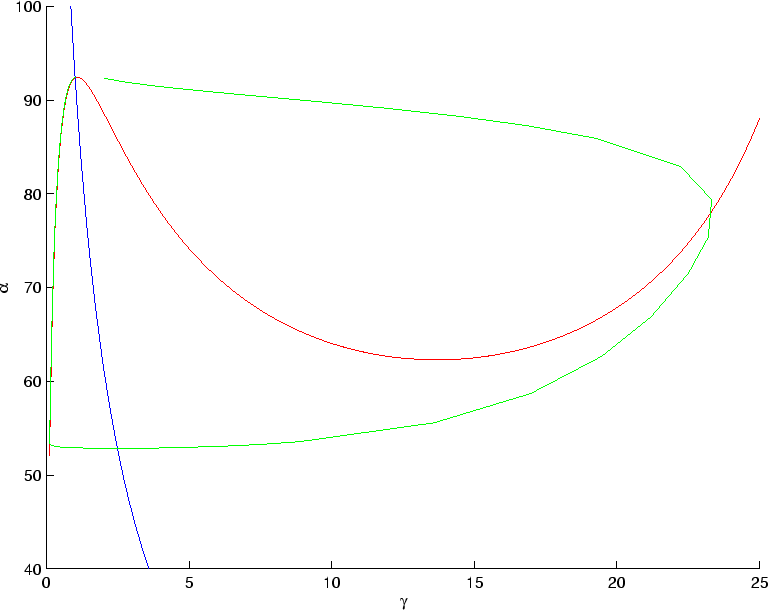
Figure 6 shows the nullclines for 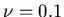 .
Using rhs_alpha.m and rhs_gamma.m, verify that the following hold:
.
Using rhs_alpha.m and rhs_gamma.m, verify that the following hold:
-
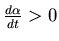 to the left of the
to the left of the 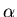 -nullcline
-nullcline
-
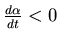 to the right of the
to the right of the 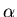 -nullcline
-nullcline
-
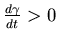 above the
above the 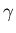 -nullcline
-nullcline
-
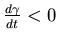 below the
below the 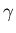 -nullcline.
-nullcline.
Note that the 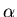 -nullcline intersects the
-nullcline intersects the 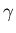 nullcline
to the right of the local maximum.
This figure also shows the superimposed stable periodic orbit.
Compare this figure to Figure 6 of
Tutorial 2. One of
nullcline
to the right of the local maximum.
This figure also shows the superimposed stable periodic orbit.
Compare this figure to Figure 6 of
Tutorial 2. One of 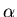 and
and 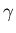 can be
thought of as a slow variable, and the other as a fast variable (although
not as fast as
can be
thought of as a slow variable, and the other as a fast variable (although
not as fast as 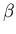 ). Which is which?
). Which is which?
Figure 6:
The nullclines for equations (7,8)
for
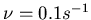 . The blue line is the
. The blue line is the 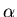 -nullcline, and the
red line is the
-nullcline, and the
red line is the 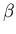 -nullcline. The stable periodic orbit is shown
in green (the transient behavior is not plotted).
-nullcline. The stable periodic orbit is shown
in green (the transient behavior is not plotted).
 |
On the other hand, Figure 7 shows the nullclines for
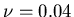 . Here the full transient behavior is included. Note
that the
. Here the full transient behavior is included. Note
that the 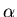 -nullcline intersects the
-nullcline intersects the 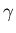 -nullcline to the
left of the local maximum.
-nullcline to the
left of the local maximum.
Figure 7:
The nullclines for equations (7,8)
for
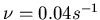 .
The blue line is the
.
The blue line is the 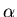 -nullcline, and the red line is the
-nullcline, and the red line is the
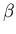 -nullcline. The trajectory is shown in green.
-nullcline. The trajectory is shown in green.
 |
Why is it that for
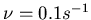 stable, periodic oscillations are
possible, while for
stable, periodic oscillations are
possible, while for
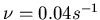 they are not? The key is how the
nullclines intersect. At this intersection, both
they are not? The key is how the
nullclines intersect. At this intersection, both  and
and 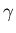 are constant. In the language of dynamical systems, this is a fixed point.
But this fixed point could be stable or unstable. Convince yourself that
when the nullclines intersect as in Figure 6 the
fixed point is unstable, whereas when the nullclines intersect as in
Figure 7 the fixed point is stable.
are constant. In the language of dynamical systems, this is a fixed point.
But this fixed point could be stable or unstable. Convince yourself that
when the nullclines intersect as in Figure 6 the
fixed point is unstable, whereas when the nullclines intersect as in
Figure 7 the fixed point is stable.
A system which has a stable fixed point but under sufficiently large
perturbation undergoes a large excursion before returning to the fixed
point is called excitable. This is the case for
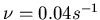 .
Referring to Figure 7, what is the simple graphical
way to determine if a given perturbation will lead to a large excursion
before returning to the fixed point?
.
Referring to Figure 7, what is the simple graphical
way to determine if a given perturbation will lead to a large excursion
before returning to the fixed point?
Comparing the material covered in this tutorial and that covered in
Tutorial 2, we see that the dynamics of squid giant axons and slime
molds apparently have some very nice qualitative similarities.



Next: About this document ...
Up: APC591 Tutorial 4: From
Previous: Reduction to a Two-Dimensional
Jeffrey M. Moehlis
2001-10-10
![]() .
Using rhs_alpha.m and rhs_gamma.m, verify that the following hold:
.
Using rhs_alpha.m and rhs_gamma.m, verify that the following hold:


![]() .
Referring to Figure 7, what is the simple graphical
way to determine if a given perturbation will lead to a large excursion
before returning to the fixed point?
.
Referring to Figure 7, what is the simple graphical
way to determine if a given perturbation will lead to a large excursion
before returning to the fixed point?