


Next: Bursting Behavior
Up: APC591 Tutorial 3: The
Previous: A Simple Model Showing
From our numerical simulations, we see that the variable 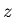 does not
vary quickly during either the rest or the active states. Mathematically,
this is due to the fact that
does not
vary quickly during either the rest or the active states. Mathematically,
this is due to the fact that 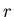 was taken to be very small.
This leads
us to consider the two-dimensional system of equations where
was taken to be very small.
This leads
us to consider the two-dimensional system of equations where
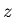 is treated as a constant:
is treated as a constant:
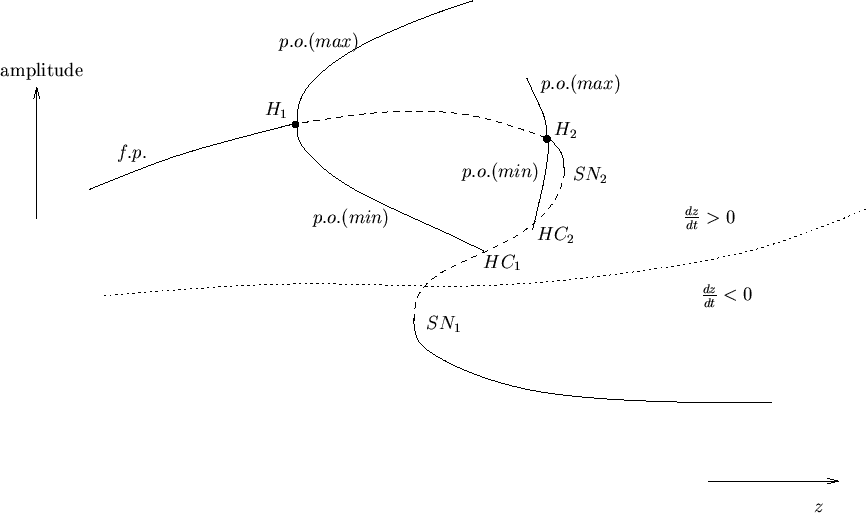
Figure 5 is a sketch of the results of a numerical bifurcation
analysis for these equations, where we take 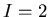 and
and 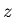 is treated as a
bifurcation parameter.
is treated as a
bifurcation parameter.
Figure 5:
Bifurcation diagram for equations (6,7) with
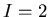 and
and 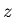 treated as a bifurcation parameter. Solid lines indicate
stable solutions, while dashed lines indicate unstable solutions. Fixed
points are labelled
treated as a bifurcation parameter. Solid lines indicate
stable solutions, while dashed lines indicate unstable solutions. Fixed
points are labelled  , and periodic orbits are labelled
, and periodic orbits are labelled 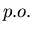 . The
dotted line shows where
. The
dotted line shows where 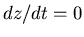 from equation (5).
from equation (5).
 |
The bifurcations for 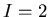 are as follows:
are as follows:
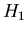 : Hopf bifurcation at
: Hopf bifurcation at 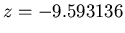
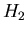 : Hopf bifurcation at
: Hopf bifurcation at 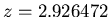
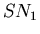 : saddlenode bifurcation of fixed points at
: saddlenode bifurcation of fixed points at 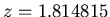
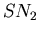 : saddlenode bifurcation of fixed points at
: saddlenode bifurcation of fixed points at 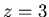
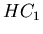 : homoclinic bifurcation at
: homoclinic bifurcation at 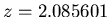
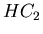 : homoclinic bifurcation at
: homoclinic bifurcation at 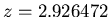



Next: Bursting Behavior
Up: APC591 Tutorial 3: The
Previous: A Simple Model Showing
Jeffrey M. Moehlis
2001-10-03
![]() does not
vary quickly during either the rest or the active states. Mathematically,
this is due to the fact that
does not
vary quickly during either the rest or the active states. Mathematically,
this is due to the fact that ![]() was taken to be very small.
This leads
us to consider the two-dimensional system of equations where
was taken to be very small.
This leads
us to consider the two-dimensional system of equations where
![]() is treated as a constant:
is treated as a constant:
![]() and
and ![]() is treated as a
bifurcation parameter.
is treated as a
bifurcation parameter.

![]() are as follows:
are as follows: