


Next: About this document ...
Up: APC591 Tutorial 2: FitzHugh's
Previous: The Periodic Orbit and
A qualitative model which captures the behavior of the Hodgkin/Huxley
equations (and equations (2) and (3)) is given by
the FitzHugh-Nagumo equations:
where
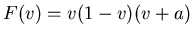 ,
,
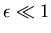 ,
and
,
and 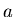 ,
, 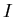 , and
, and 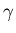 are constants. These equations have the
advantage over equations (2) and (3) that the righthand
sides are simpler functions. The FitzHugh-Nagumo equations have been used
to qualitatively model many biological phenomena (see, for example,
Mathematical Physiology by J. Keener and J. Sneyd, on reserve in the
library).
are constants. These equations have the
advantage over equations (2) and (3) that the righthand
sides are simpler functions. The FitzHugh-Nagumo equations have been used
to qualitatively model many biological phenomena (see, for example,
Mathematical Physiology by J. Keener and J. Sneyd, on reserve in the
library).
Using the programs given in this tutorial as models, use Matlab to draw
the nullclines and solve the FitzHugh-Nagumo equations for 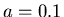 ,
,
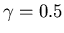 , and different values of
, and different values of 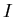 .
.
Jeffrey M. Moehlis
2001-09-24
![]() ,
,
![]() , and different values of
, and different values of ![]() .
.