First, recall that the equations for the gating variables can be
solved exactly if ![]() is held constant. For example, if
is held constant. For example, if ![]() , then
, then
We see that the time constant ![]() is much smaller than
is much smaller than ![]() or
or
![]() over the entire range of interest of
over the entire range of interest of ![]() . This means that the
. This means that the ![]() variable evolves faster than the
variable evolves faster than the ![]() or
or ![]() variables. This suggests that
we might be able to replace
variables. This suggests that
we might be able to replace ![]() in the Hodgkin/Huxley model by
in the Hodgkin/Huxley model by
![]() , i.e., use the instantaneous value of
, i.e., use the instantaneous value of ![]() to compute
to compute
![]() , then use this for
, then use this for ![]() in the righthand sides of the
in the righthand sides of the
![]() ,
, ![]() , and
, and ![]() equations. The appropriateness of this
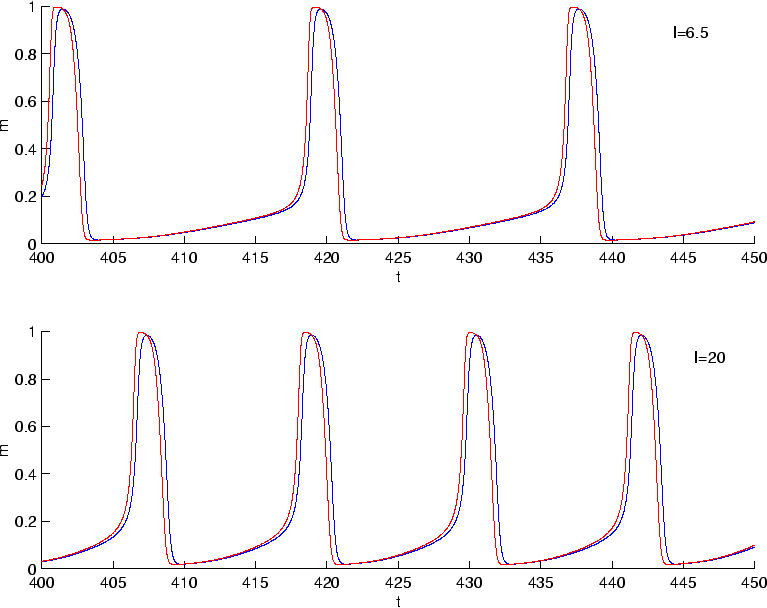
approximation is illustrated in Figure 2. This shows
the timeseries for input currents of
equations. The appropriateness of this
approximation is illustrated in Figure 2. This shows
the timeseries for input currents of
![]() and
and
![]() after the transient behavior has decayed away.
after the transient behavior has decayed away.
 |
The code used to generate this plot can't be given here because of its similarity to the code you're writing for Homework #1. It should be relatively easy to modify your own code to generate a similar plot - you're encouraged to try this, and also to write appropriate code to generate Figure 1.