Introduction

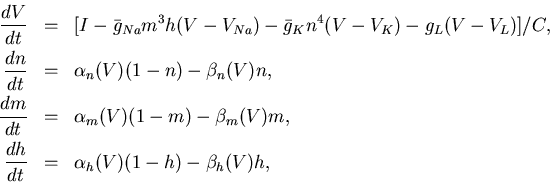
The Hodgkin/Huxley equations using modern conventions for the space clamped membrane are given by

$$\begin{eqnarray*} \frac{dV}{dt} &=& [I - \bar{g}_{Na} m^3 h (V-V_{Na}) - \bar{g}... ...m(V) m, \\ \frac{dh}{dt} &=& \alpha_h(V) (1-h) - \beta_h(V) h, \end{eqnarray*}$$

where

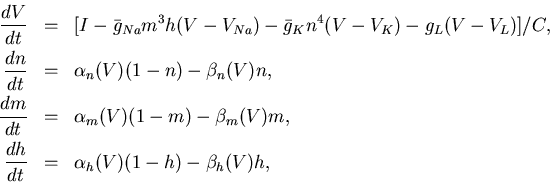
$$\begin{eqnarray*} \alpha_n(V) = \frac{0.01 (V+55)}{1-\exp[-(V+55)/10]}, && \beta... ... \exp[-(V+65)/20], && \beta_h(V) = \frac{1}{1+\exp[-(V+35)/10]}. \end{eqnarray*}$$

As described in lecture, $V$ is the transmembrane potential, $I$ is the current injected into the neuron from a microelectrode, and $n$, $m$, and $h$ are dimensionless gating variables. In these equations, voltages are measured in $mV$, current density in $\mu A/cm^2$, capacitance density in $\mu F/cm^2$, and time in $msec$. The values of the constants at $6.3^\circ C$ are

$$\bar{g}_{Na} = 120 \; mmho/cm^2, \qquad \bar{g}_K=36 \; mmho/cm^2, \qquad g_L=0.3 \; mmho/cm^2,$$

$$V_{Na} = \; 50 mV, \qquad V_K = -77 \; mV, \qquad V_L = -54.4 \; mV, \qquad C = 1 \; \mu F/cm^2.$$

It was shown by R. FitzHugh that these equations can be reduced to a two-dimensional system of equations whose dynamics approximate the dynamics of the full four-dimensional Hodgkin/Huxley model quite well. This reduction also helps to give an intuitive understanding of the dynamics. In this computer lab, we will explore FitzHugh's reduction, using Matlab where appropriate. For more detail and references, see the book Mathematical Physiology by J. Keener and J. Sneyd, on reserve in the library.