


Next: Oscillations and Excitability
Up: APC591 Tutorial 4: From
Previous: Introduction
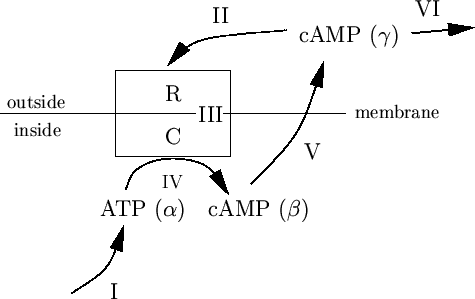
Goldbeter and Segel's model for the dynamic behavior of the cAMP signalling
system for Dictyostelium discoideum is sketched in
Figure 1. The steps are as follows:
- I: synthesis of ATP
- II: binding of extracellular cAMP to the receptor (labelled R)
- III: activation of adenylate cyclase (labelled C)
- IV: production of cAMP from ATP, catalyzed by adenylate cyclase
- V: transport of cAMP into the extracellular medium
- VI: cAMP hydrolysis by phosphodiesterase
Figure 1:
Sketch of Goldbeter and Segel's model of the cAMP signalling system
for Dictyostelium discoideum.
 |
The variables in the model are dimensionless concentrations of the
intracellular ATP (called 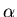 ), the intracellular cAMP (called
), the intracellular cAMP (called 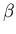 ),
and the extracellular cAMP (called
),
and the extracellular cAMP (called 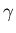 ).
Assuming that the system remains spatially homogeneous (which corresponds
to conditions in continuously stirred suspensions), the time evolution
of the system is governed by a three-dimensional set of ODES:
).
Assuming that the system remains spatially homogeneous (which corresponds
to conditions in continuously stirred suspensions), the time evolution
of the system is governed by a three-dimensional set of ODES:
where the rate function 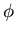 for adenylate cyclase is given by
for adenylate cyclase is given by
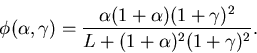 |
(4) |
The definitions for the constants
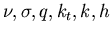 , and
, and 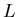 are
given in Goldbeter and Segel. For our purposes, the important things are:
are
given in Goldbeter and Segel. For our purposes, the important things are:
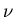 in (1) represents the (constant) synthesis of ATP
in (1) represents the (constant) synthesis of ATP
-
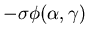 in (1) and
in (1) and
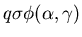 in (2) represent the production of
intracellular cAMP from ATP
in (2) represent the production of
intracellular cAMP from ATP
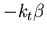 in (2) and
in (2) and 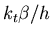 in (3) represent
the transport of cAMP into the extracellular medium
in (3) represent
the transport of cAMP into the extracellular medium
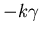 in (3) represents the hydrolysis of extracellular
cAMP by phosphodiesterase.
in (3) represents the hydrolysis of extracellular
cAMP by phosphodiesterase.
Following Goldbeter and Segel, the constants will be taken to be
We will consider different values of 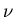 , the rate of synthesis of ATP.
, the rate of synthesis of ATP.



Next: Oscillations and Excitability
Up: APC591 Tutorial 4: From
Previous: Introduction
Jeffrey M. Moehlis
2001-10-10


![]() ), the intracellular cAMP (called
), the intracellular cAMP (called ![]() ),
and the extracellular cAMP (called
),
and the extracellular cAMP (called ![]() ).
Assuming that the system remains spatially homogeneous (which corresponds
to conditions in continuously stirred suspensions), the time evolution
of the system is governed by a three-dimensional set of ODES:
).
Assuming that the system remains spatially homogeneous (which corresponds
to conditions in continuously stirred suspensions), the time evolution
of the system is governed by a three-dimensional set of ODES: