


Next: A Simple Model Showing
Up: APC591 Tutorial 3: The
Previous: Fixed Points and Periodic
Next, we need to understand how fixed points and periodic orbits change
as parameters are varied.
It is possible that at some particular set of parameters a fixed point
or periodic orbit is stable, but at a different set it is unstable.
Such a change in stability under a change in parameters is an example of
a bifurcation. Another example of a bifurcation is when, as parameters
are changed, new fixed points or periodic orbits come into existence.
Loosely speaking, a bifurcation is a qualitative change in the dynamics
of the system of ODEs as a parameter varies. We now give several
examples of bifurcations. We show the flow of the vector fields in
phase space, that is, the space of the variables 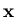 . The
bifurcation diagrams summarize the behavior near the bifurcation; solid
lines show stable solutions, while dashed lines show unstable solutions.
. The
bifurcation diagrams summarize the behavior near the bifurcation; solid
lines show stable solutions, while dashed lines show unstable solutions.
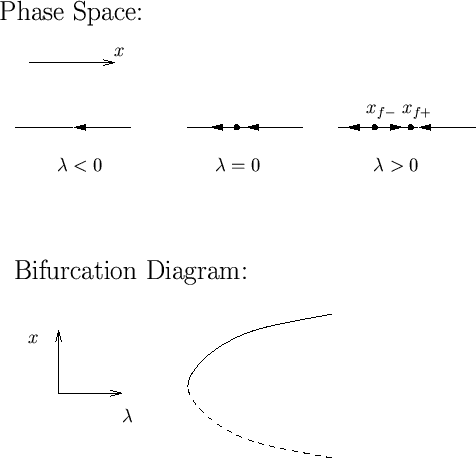
Saddlenode bifurcation:
Consider the one-dimensional differential equation
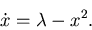 |
(2) |
It is readily shown that no fixed points exist for 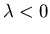 , but
fixed points
, but
fixed points
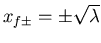 exist for
exist for 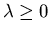 .
.
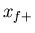 is stable, while
is stable, while 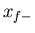 is unstable. The qualitative change
in behavior at
is unstable. The qualitative change
in behavior at 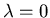 is called a saddlenode bifurcation.
is called a saddlenode bifurcation.
Figure 1:
Top: Fixed points and flow for equation (2). Bottom:
Bifurcation diagram for the saddlenode bifurcation.
 |
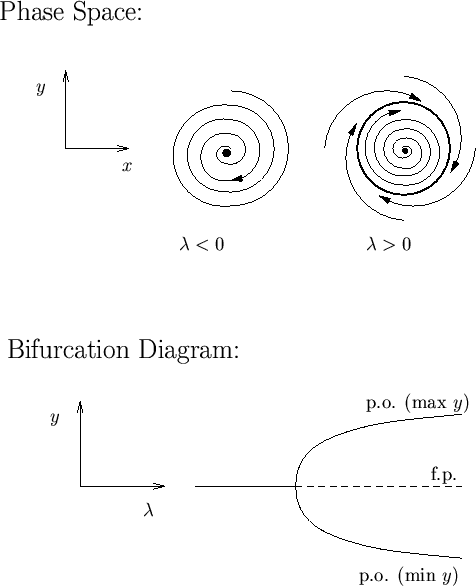
Hopf bifurcation: A Hopf bifurcation involves the change in
stability of a fixed point of a dynamical system together with the birth of a
periodic orbit. For example, for the Hopf bifurcation shown in Figure
2, for 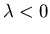 there is a stable fixed point, while for
there is a stable fixed point, while for
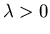 there is an unstable fixed point and a stable periodic orbit.
there is an unstable fixed point and a stable periodic orbit.
Figure 2:
Top: Phase space for an example of a Hopf bifurcation. Bottom:
Bifurcation diagram for the Hopf bifurcation. In this diagram, both the
maximum and the minimum values of 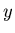 on the periodic orbit are shown.
on the periodic orbit are shown.
 |
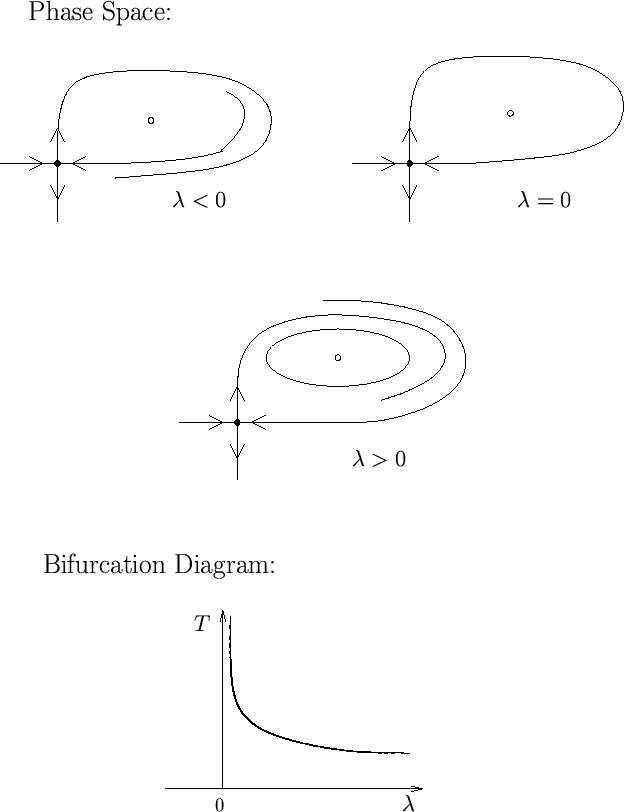
Homoclinic bifurcation: A homoclinic orbit is a trajectory which
approaches a fixed point both as
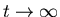 and as
and as
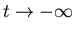 . The formation of a homoclinic orbit as a
parameter is varied, called a homoclinic bifurcation, can lead
to the creation or destruction of a periodic orbit. For the homoclinic
bifurcation shown in Figure 3, a homoclinic orbit forms at
. The formation of a homoclinic orbit as a
parameter is varied, called a homoclinic bifurcation, can lead
to the creation or destruction of a periodic orbit. For the homoclinic
bifurcation shown in Figure 3, a homoclinic orbit forms at
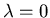 , and a periodic orbit exists for
, and a periodic orbit exists for 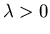 but not for
but not for
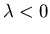 . As
. As
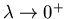 , the period
, the period 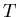 of the
periodic orbit diverges to infinity.
of the
periodic orbit diverges to infinity.
Figure 3:
Top: Phase space and bifurcation diagram for a homoclinic bifurcation
giving birth to a stable periodic orbit as 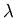 increases through 0.
The open dots show fixed points which do not participate in the bifurcation.
Bottom: Bifurcation diagram showing the period of the periodic orbit as
a function of
increases through 0.
The open dots show fixed points which do not participate in the bifurcation.
Bottom: Bifurcation diagram showing the period of the periodic orbit as
a function of 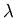 .
.
 |



Next: A Simple Model Showing
Up: APC591 Tutorial 3: The
Previous: Fixed Points and Periodic
Jeffrey M. Moehlis
2001-10-03
![]() . The
bifurcation diagrams summarize the behavior near the bifurcation; solid
lines show stable solutions, while dashed lines show unstable solutions.
. The
bifurcation diagrams summarize the behavior near the bifurcation; solid
lines show stable solutions, while dashed lines show unstable solutions.

![]() there is a stable fixed point, while for
there is a stable fixed point, while for
![]() there is an unstable fixed point and a stable periodic orbit.
there is an unstable fixed point and a stable periodic orbit.

