Numerically Solving the Example with Euler's Method

Although we know the exact solution for equation (5), it is instructive to consider its numerical solution using Euler's method. This is implemented in Matlab with the following series of statements (note that we compare to the exact solution, so to run this program you must have the file ``yexact.m'' as described on the last page):

% Example: Euler's method for dy/dt = K*(y-s)
K = 1;
s = 20;
y0 = 100;

npoints = 50;
dt = 0.1;

y = zeros(npoints,1); % this initializes the vector y to being all zeros
t = zeros(npoints,1);

y(1) = y0; % the initial condition
t(1) = 0.0;

for step=1:npoints-1 % loop over the timesteps
y(step+1) = y(step) + dt*K*(y(step)-s);
t(step+1) = t(step) + dt;
end

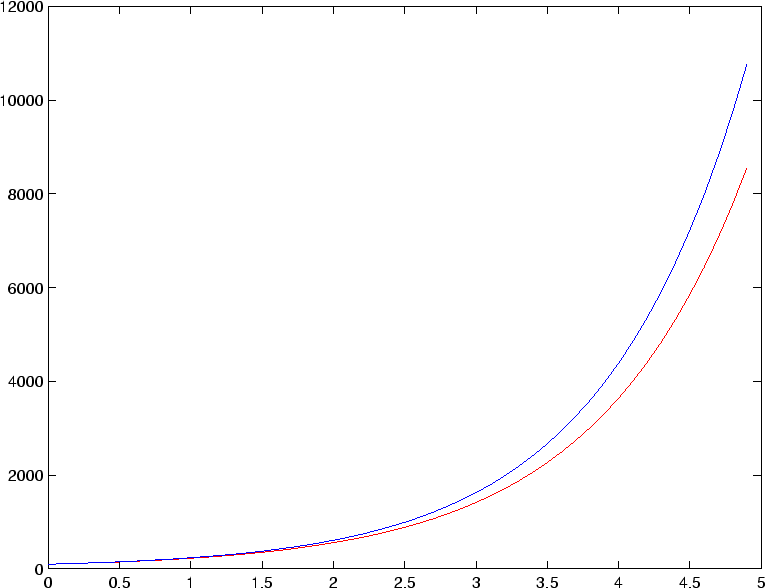
plot(t,y,'r'); %plots the numerical solution in red
hold on; %keep the previously plotted lines
plot(t,yexact(t,y0,K,s)); %plots the exact solution (default plot is in blue, solid line)

Text version of this program

This produces Figure 2:

Figure 2: The exact solution (blue) and numerical solution from Euler's method (red) for equation (5) with $y_0=100$, $K = 1$, $s=20$.

Although the numerical solution behaves qualitatively in the correct way, it is not very accurate quantitatively. Try modifying the stepsize in the above program to see how this affects the accuracy.