Next: An Example
Up: APC591 Tutorial 1: Euler's
Previous: Introduction
Consider the initial value problem
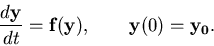 |
(1) |
Suppose we write the Taylor exansion of the solution:
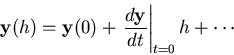 |
(2) |
Truncating and using (1), we obtain the formula for Euler's method
for the numerical solution of differential equations:
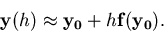 |
(3) |
Of course, there is nothing special about 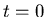 , so, letting
, so, letting
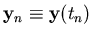 ,
,
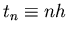 , we obtain
, we obtain
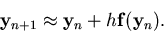 |
(4) |
By iterating, we find an approximation to the solution 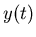 of (1).
Here
of (1).
Here 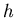 is known as the stepsize.
is known as the stepsize.
Jeffrey M. Moehlis
2001-09-24