Fluid Mechanics of Miscible Interfaces

Understanding the dynamical evolution of interfaces between fluids remains a key challenge in fluid dynamics research. In recent years, there has been a renewed focus on the potential role of non-conventional, so-called Korteweg stresses in miscible fluid flows with steep concentration gradients. These stresses, which were first postulated a century ago, are not accounted for by the commonly used sets of conservation equations. In fact, it is still uncertain how they can be modelled mathematically. In order to obtain some insight in this direction, our group has been carrying out high-accuracy simulations that incorporate these stresses based on approaches suggested in the recent literature. In adition, we are performing linear stability analyses as well. The simulations and stability results have been compared with corresponding experiments, in order to assess the validity of the postulated stress terms. These comparisons indicate that Korteweg stresses are indeed important in some parameter ranges of interest in a variety of applications. However, detailed quantitative information cannot be obtained yet, due to the limitations earthbound laboratories impose on the experimental component of the program. As a result, jointly with our colleagues at USC and ESPCI, we are now preparing an International Space Station based investigation to carry this work further.

Two-way Coupling Effects in Particle Laden Flows

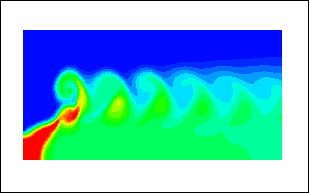
The mechanisms by which suspended particles affect the motion of the carrier fluid for the most part are still poorly understood. Our research in this area focuses on two applications in which the suspension is relatively dilute. The first one of these concerns particle laden mixing layers, for which we have investigated the effects of particle inertia on the linear stability and nonlinear growth of the Kelvin-Helmholtz instability. In this area, our work has provided new insight into the effcts of the particular phase on the vorticity dynamics of the carrier fluid, which drives the instability. For small values of the dimensionless Stokes number, a mild destabilization of the mixing layer is observed. At moderate and large Stokes numbers, on the other hand, the vorticity transport from the braids into the cores of the evolving vortices is seen to be slowed by the two-way coupling effects. For constant mass loadings, the two-way coupling effects are strongest at intermediate Stokes numbers.

The second application concerns particle driven gravity currents, such as turbidity currents in the ocean. Here we were, jointly with our colleagues at ETH Zurich, the first ones to carry out high-resolution, three-dimensional direct numerical simulations of such sedimenting currents, based on an Eulerian transport equation for the suspended phase. The simulations show that, while two-dimensional models can predict the flow development at early times, the long time behavior is dominated by three-dimensional effects, such as the breakdown of large scale spanwise vortices. By taking these three-dimensional effects into account, time-dependent sediment profiles are obtained that are in close agreement with available experimental data.

Direct Numerical Simulations of Porous Media Flows

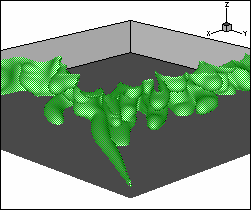
The dynamics of two-phase flows in porous media, e.g. in enhanced oil recovery, is dominated by a multitude of physical mechanisms and parameters. Among the most important ones are the viscosity and density ratios of the fluids, and the correlation lengths and heterogeneity levels of the porous medium. We have employed the tool of three-dimensional direct numerical simulations in order to investigate the dynamical interplay between the governing physical mechanisms. In this process, we have focused not only on the semi-infinite, rectilinear geometry, but also on the more complex quarter five-spot arrangement of injection and production wells. Among our main findings has been the derivation of scaling laws for the emerging gravity tongue, as well as the observation that intermediate levels of heterogeneity can lead to optimal recovery results, since the tendencies towards 'channeling' and towards the formation of a gravity tongue are minimized.

The Dynamics of Swirling Jets

This work aims at achieving an understanding of the mechanisms behind axisymmetric vortex breakdown, and behind the transition from axisymmetric to 'spiral' or helical vortex breakdown structures. In particular, our goal is to put to the test recent hypotheses regarding the role that an absolute instability mechanism might play in this regard. Towards this end, we have been employing three-dimensional direct numerical simulations of the Navier-Stokes equations in cylindrical coordinates. These simulations show that for sufficiently large swirl numbers, the initial breakdown is followed by the formation of an axisymmetric, quasisteady velocity field. In the wake region of the primary breakdown bubble, a finite region of absolute instability is observed to exist, which subsequently gives rise to the formation of a temporally periodic helical instability. This finding hence suggests that the transition from axisymmetric to helical breakdown is a manifestation of a global mode instability.