Introduction

In this computer lab we'll consider some generalizations to the epidemiological models covered in the lectures. The motivation for these generalizations will be the fact that for some diseases the number of infected individuals 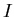$I$ in a population oscillates seasonally. For example, childhood diseases such as measles and rubella increase each winter because of increased contact between children at school. Specifically, we'll explore what happens when the contact rate is a periodic function of time. 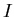It will be shown for a simple SIS model (which is very similar to the SIR model covered by Professor Levin except that recovered individuals return to class S instead of passing to class R) that such a periodic contact rate can lead to a periodic oscillation in $I$ with the same period as the contact rate. For more complicated models, it is possible to get states in which the period of 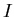$I$ is some integer multiple of the period of the contact rate. In fact, as parameters are varied it is possible for some models to get a period doubling cascade to chaotic behavior.