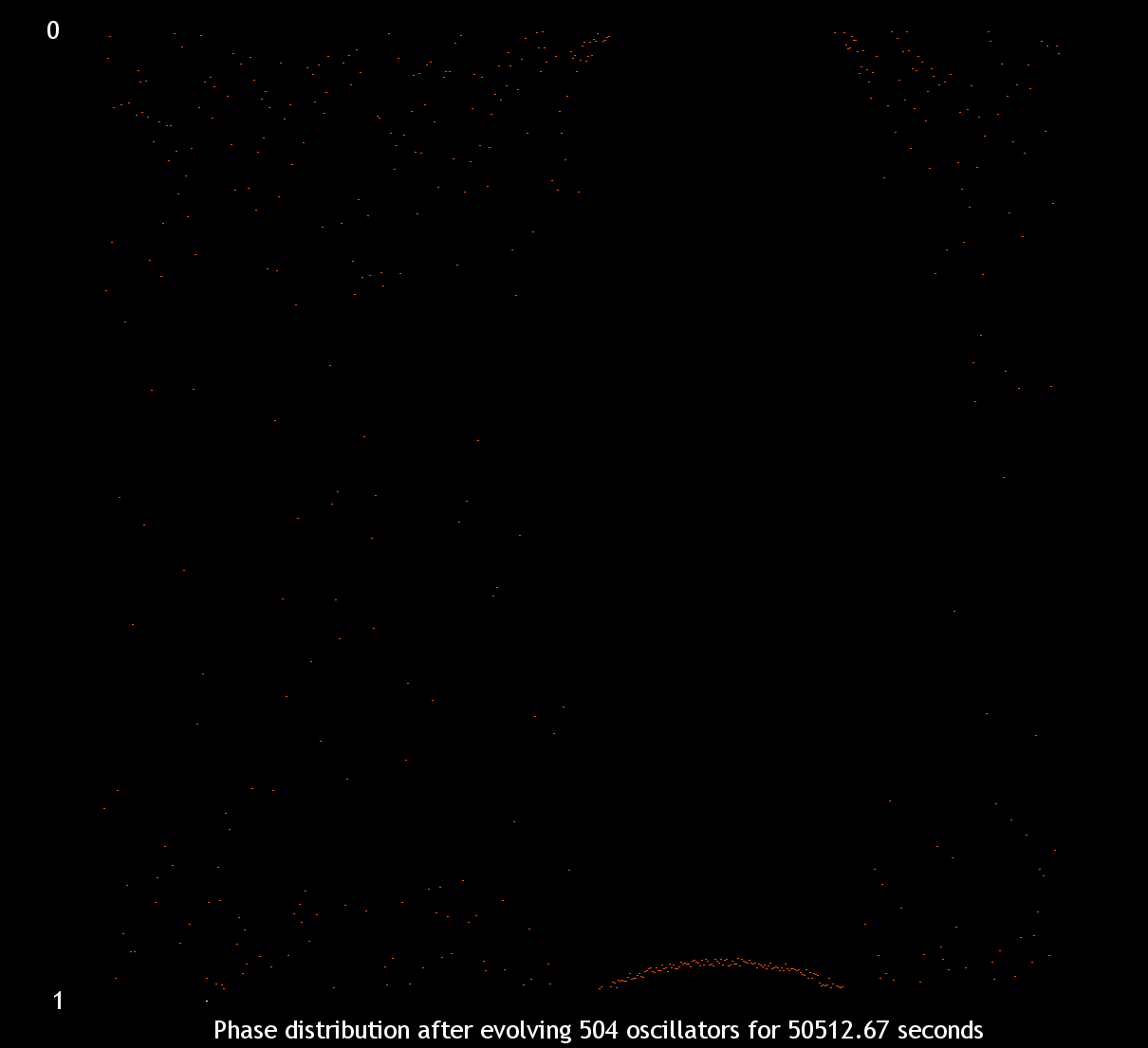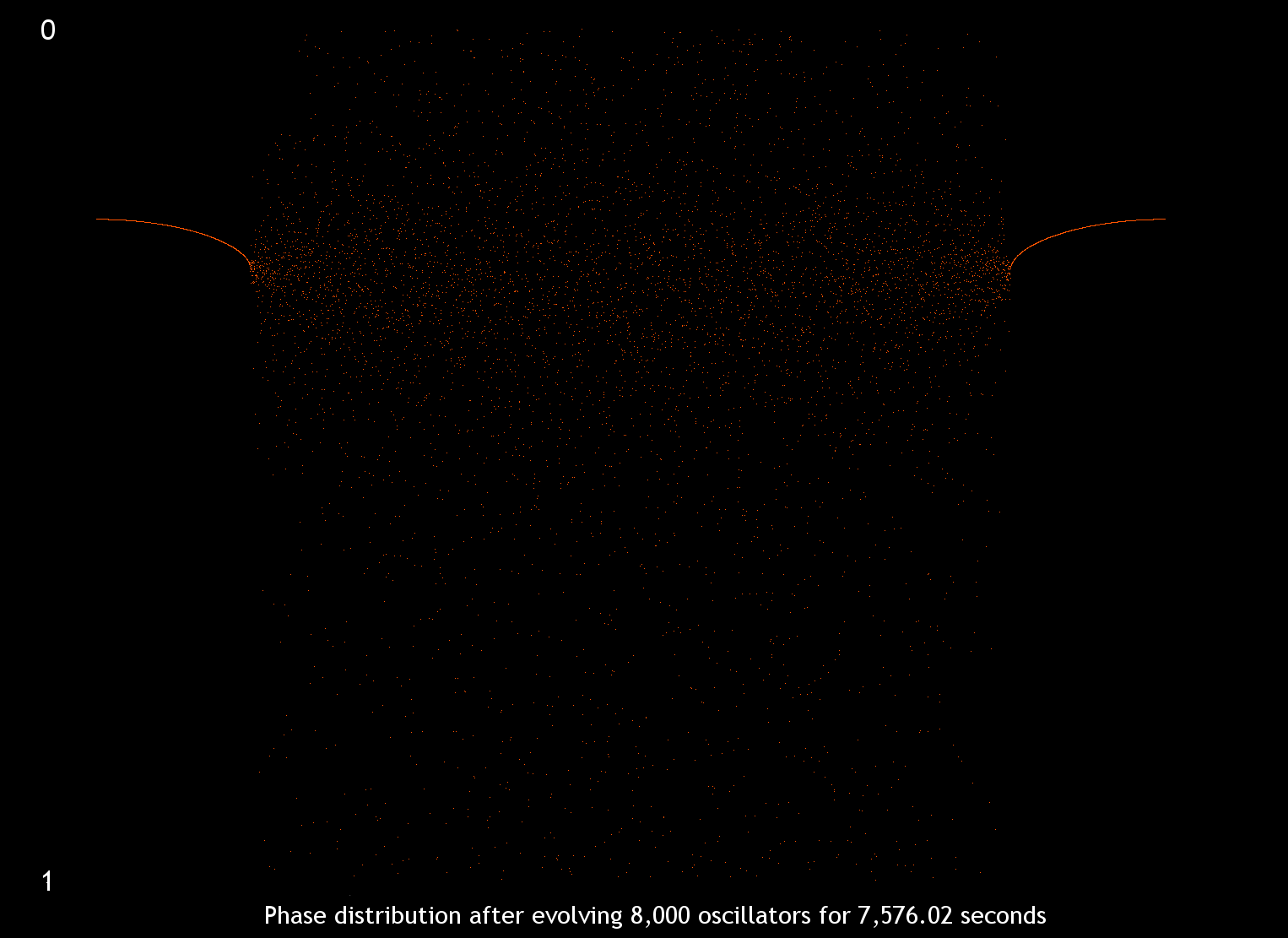We show some examples of chimera states in phase oscillator networks. All of these examples were computed
using prism software. In all cases, we used Runge-Kutta 4th order, a time step 0.01 and long double precision.
Apart from regarding phases as defined on [0,1], we generally follow the conventions of
Abrams and Strogatz' paper (Chimera States in a ring of nonlocally coupled oscillators, Int. Jnr. of Bifurcation
and Chaos, 16 (1) (2000), 21-37). In particular we use an exponential kernel (with κ=4) and
take α=1.45. Unless stated to the contrary we assume all phase oscillators
have frequency term equal 0. We initialize using Kuramoto's protocol (see Abrams and Strogatz for details).
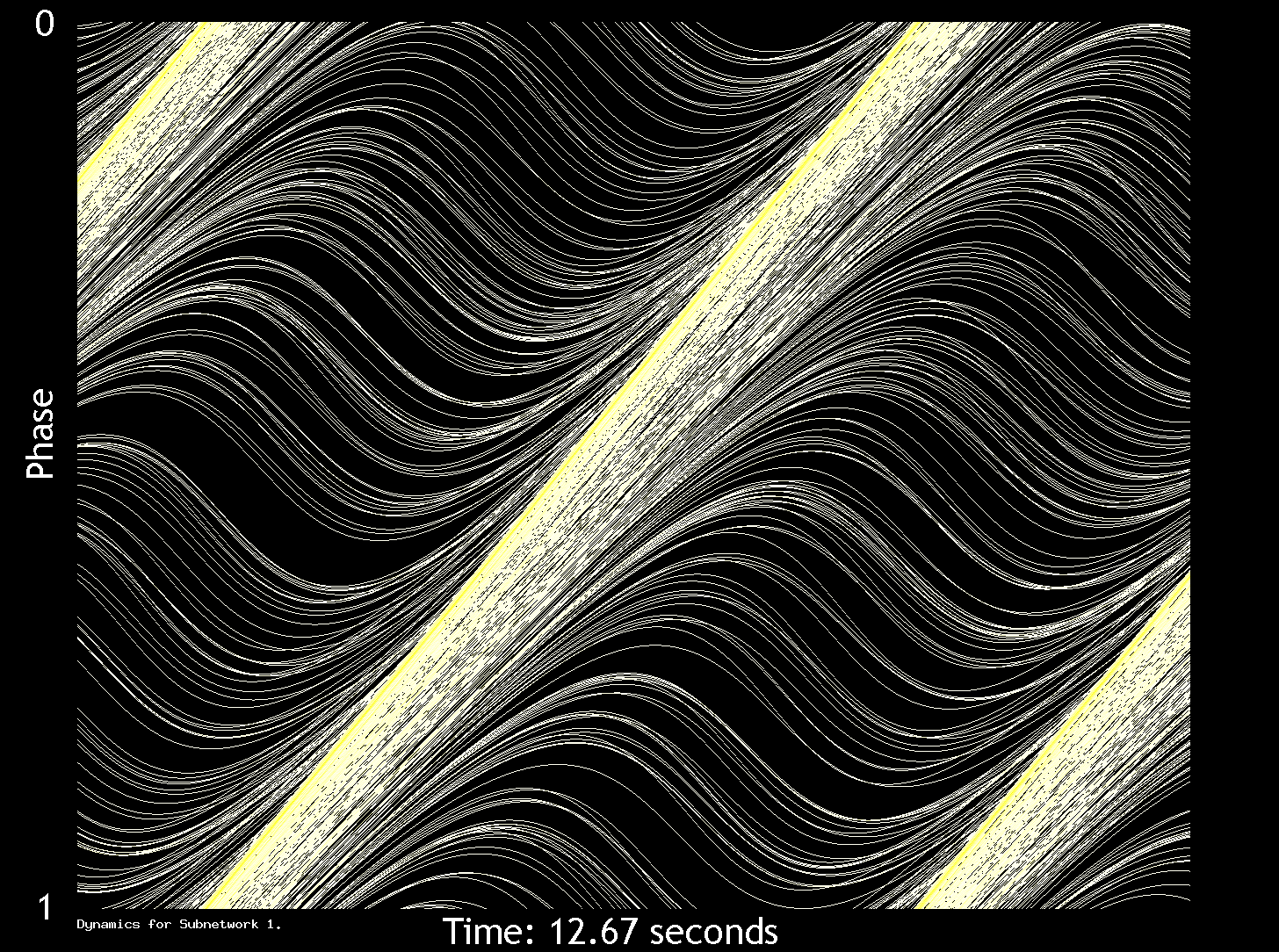
In Figure 1, we show the collective dynamics of 1000 phase oscillators over a time period of 12.67 seconds after allowing the system to evolve for
10,000 seconds (about 2.77 hours)
Figure 1. Collective Dynamics over 12.67 seconds
In Figure 2, we show the Chimera state after 10,012.67 seconds of system evolution.
Figure 2. Chimera State
Next we show what happens if we allow the frequency of the individual phase oscillators to be set randomly and uniformly
within the range ±0.001. For these examples we take 504 oscillators. In figures 3 and 4 we show the result
after evolving the system for 10,000 seconds. In figure 5, we show the chimera state after evolving for an
additional 40,500 seconds.
Figure 3. Collective Dynamics over 12.67 seconds
Figure 4. Chimera State
Figure 5. Chimera State after 50,512.67 seconds (about 14 hours)
Finally we show collective dynamics and chimera state for a system of 8,000 phase oscillators
after evolving the system for 7576.02 seconds (just over two hours).
Figure 6. Collective Dynamics of 8,000 oscillators over 12.67 seconds
Figure 7. Chimera State
Video
- Chimera state movie (animated gif format).
The movie shows the evolution of a chimera state for a 5000 node phase oscillator
system. Computation was Runge-Kutta 4th order with a time step of
0.005. A frame of the chimera state was taken every 0.125 seconds.
(Best viewed using a viewer with *no* post processing or anti-aliasing features.)
Research supported by NSF Grants DMS-0806321 and DMS-1265253.
All images and movies copyright Michael Field, 2013. Images and Movies may be
not be used without my written permission.
Research supported in part by DMS-0806321 and DMS-1265253 and in collaboration with Christian Bick.
Software using net programs and including some components based on ATLAS and CBLAS
libraries as well as custom long double precision software.
email: mikefield@gmail.com
Professor Mike Field
Department of Mechanical Engineering
University of California
Santa Barbara, CA 93106
|