Banded radiation solver
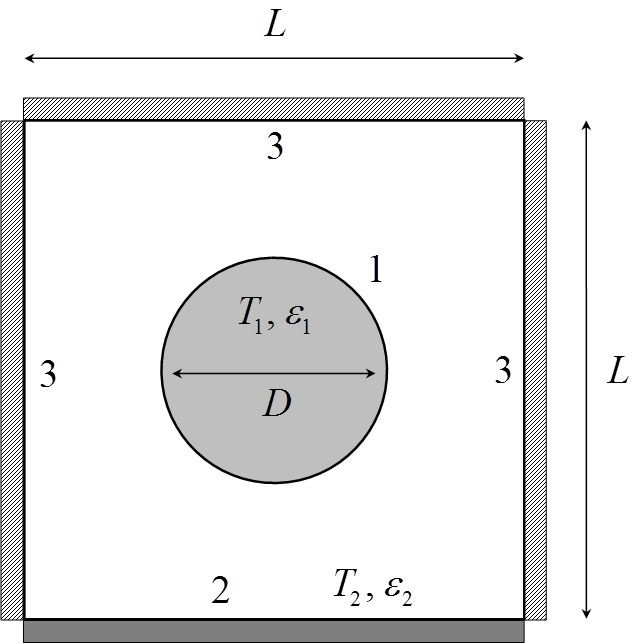 A long cylinder
is held at a temperature of T1=1000 K in the long square duct shown.
The edge dimension of the square duct is L=1 m, and three of the four walls are
insulated. The fourth wall is held at a temperature of T2=500 K and
has an emissivity of ε2=0.2. The cylinder has a diameter D=L/2
and an emissivity of ε1=0.7. Treating the insulating walls of
the duct (surface-3) as isothermal, determine the net rate of radiative heat
loss from the cylinder Qrad1 using network analysis. What is the
temperature of the adiabatic walls T3? Solve this problem using the banded
radiation solver.
A long cylinder
is held at a temperature of T1=1000 K in the long square duct shown.
The edge dimension of the square duct is L=1 m, and three of the four walls are
insulated. The fourth wall is held at a temperature of T2=500 K and
has an emissivity of ε2=0.2. The cylinder has a diameter D=L/2
and an emissivity of ε1=0.7. Treating the insulating walls of
the duct (surface-3) as isothermal, determine the net rate of radiative heat
loss from the cylinder Qrad1 using network analysis. What is the
temperature of the adiabatic walls T3? Solve this problem using the banded
radiation solver.
Solution:
The problem parameters are:
L=1;
D=L/2;
T1=1000;
T2=500;
e=[0.7; 0.2; 1.];
A=[pi*D*1; L*1; 3*L*1];
The view factors for radiative exchange are calculated from:
F=zeros(3,3);
F(1,2)=1/4; % symmetry
F(1,3)=1-F(1,2); % summation rule
F(2,1)=A(1)*F(1,2)/A(2); % reciprocity
F(3,1)=A(1)*F(1,3)/A(3); % reciprocity
F(2,3)=1-F(2,1); % summation rule
F(3,2)=A(2)*F(2,3)/A(3); % reciprocity
F(3,3)=1-F(3,1)-F(3,2); % summation rule
A function that solves the banded radiation equations based on an array of guessed values for the unknown surface temperatures is defined. In this problem there is only one unknown temperature T3, and the surfaces area gray (band=[0 Inf])
qrad = @(T3)SolveBandRadEqs([T1; T2; T3],F,e,[0 Inf]);
A function that evaluates the error in guessed temperatures is defined. For this problem, the condition that surface 3 is adiabatic is the appropriate error check:
RadBalEqs = @(qrad)[qrad(3)]; % qrad(3)=0
The final step is to employ a root finding function to determine the correct surface temperatures that satisfy the error condition.
T3=NSolve(@(G)RadBalEqs(qrad(G)),700)
T3 = 968.86
Therefore, the adiabatic wall temperature is found to be T3=968.9 K. The radiative flux of heat from each surface is determined from the banded radiation equations solver:
q=SolveBandRadEqs([T1; T2; T3],F,e,[0 Inf]);
Q=q.*A
Q =
9.6075e+03
-9.6075e+03
3.4985e-06
Therefore, the net radiative heat loss of heat from the cylinder is Qrad1=9607.5 W.
Supposed surface-1 has the spectral emissivity given by:
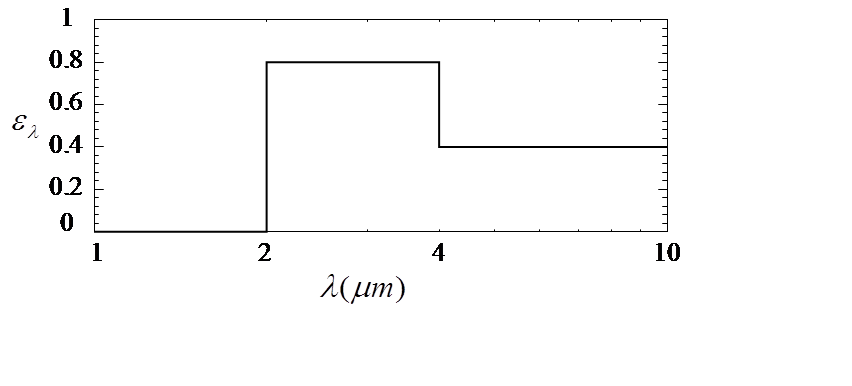
The radiation bands for this problem are defined by:
bands = [0 2 4 Inf];
and the spectral emissivities for the enclosure are defined by:
e=[0.0 0.8 0.4; ... % surface-1
0.2 0.2 0.2; ... % surface-2
1.0 1.0 1.0]; % surface-3
The function that solves the banded radiation equations is redefined:
qrad = @(T3)SolveBandRadEqs([T1; T2; T3],F,e,bands);
and solved:
T3=NSolve(@(G)RadBalEqs(qrad(G)),700)
T3 = 958.65
Therefore, the adiabatic wall temperature is now T3=958.7 K. The radiative flux of heat from each surface is determined:
q=SolveBandRadEqs([T1; T2; T3],F,e,bands);
Q=q.*A
Q =
9.1784e+03
-9.1784e+03
2.3382e-06
Therefore, the net radiative heat loss of heat from the cylinder is now Qrad1=9178.4 W.