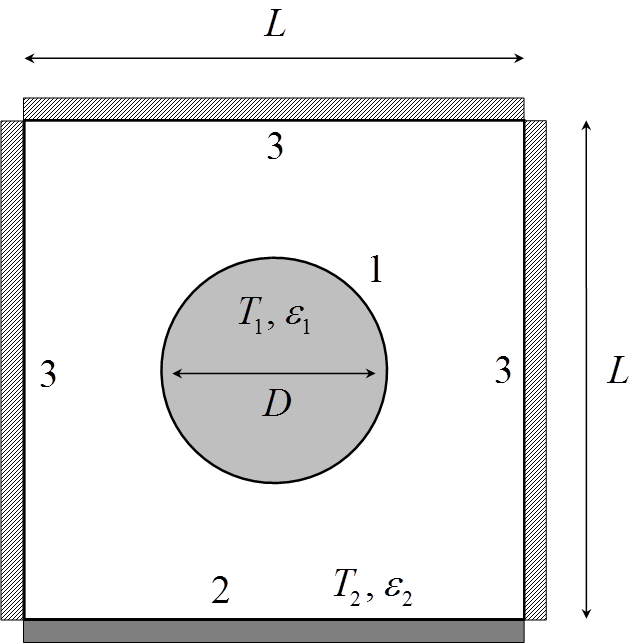
Radiation network analysis

A long cylinder is held at a temperature of T₁=1000 K in the long square duct shown. The edge dimension of the square duct is L=1 m, and three of the four walls are insulated. The fourth wall is held at a temperature of T₂=500 K and has an emissivity of ε₂=0.2. The cylinder has a diameter D=L/2 and an emissivity of ε₁=0.7. Treating the insulating walls of the duct (surface-3) as isothermal, determine the net rate of radiative heat loss from the cylinder Q_rad1 using network analysis. What is the temperature of the adiabatic walls T₃?

 

Solution:

The network for radiative exchange between the surfaces of the enclosure is given by:

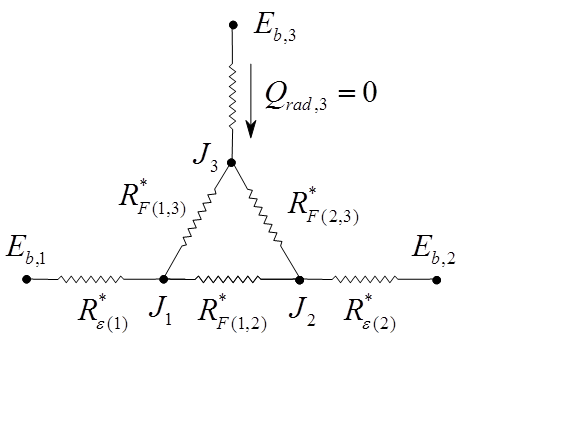where and

 

The net resistance between the cylinder potential E_b1 and the non-adiabatic wall potential E_b2 is found from:

 

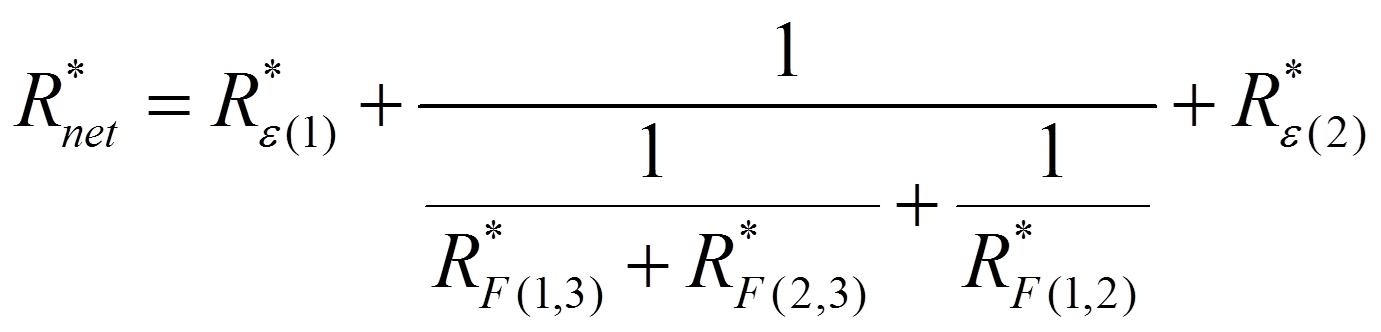
The net rate of radiative heat loss from the cylinder Q_rad1 is found from:

 

The problem is solved numerically with the following steps:

 

L=1;

D=L/2;

T1=1000;

T2=500;

e=[0.7; 0.2; 1.];

A=[pi*D*1; L*1; 3*L*1];

 

F=zeros(3,3);

F(1,2)=1/4; % symmetry

F(1,3)=1-F(1,2); % summation rule

 

F(2,1)=A(1)*F(1,2)/A(2); % reciprocity

F(3,1)=A(1)*F(1,3)/A(3); % reciprocity

 

F(2,3)=1-F(2,1); % summation rule

F(3,2)=A(2)*F(2,3)/A(3); % reciprocity

 

F(3,3)=1-F(3,1)-F(3,2); % summation rule

 

Re=(1-e)./e./A;

RF=1./repmat(A,1,size(F,2))./F;

 

Rnet=Re(1)+1/(1/(RF(1,3)+RF(3,2))+1/RF(1,2))+Re(2)

Rnet = 5.5332

 

Qrad1=(Eblk(T1)-Eblk(T2))/Rnet

Qrad1 = 9607.5

 

To find the temperature T₃ requires determining the radiosity J₃. J₁ and J₂ can first be found from:

 

J1=Eblk(T1)-Qrad1*Re(1);

J2=Eblk(T2)+Qrad1*Re(2);

 

The "current" through the J₃ node is

.

Therefore, J₃ is found from by adding the potential rise across the resistance R^*_F(2,3)

Therefore,

 

J3=J2+(J1-J2)*RF(2,3)/(RF(1,3)+RF(2,3));

 

Since surface three is adiabatic, the radiosity equals the blackbody emission. Therefore the surface temperature is found from:

 

T3=(J3/sig)^0.25

T3 = 968.86