Radiosity equation analysis

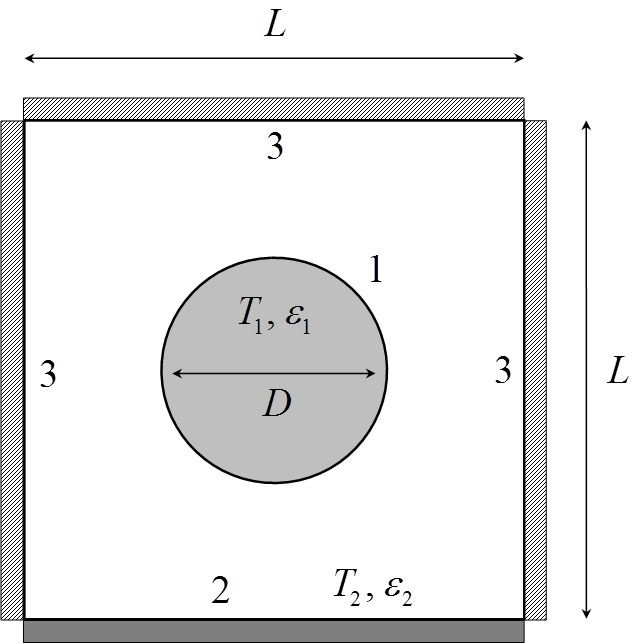A long cylinder is held at a temperature of T₁=1000 K in the long square duct shown. The edge dimension of the square duct is L=1 m, and three of the four walls are insulated. The fourth wall is held at a temperature of T₂=500 K and has an emissivity of ε₂=0.2. The cylinder has a diameter D=L/2 and an emissivity of ε₁=0.7. Treating the insulating walls of the duct (surface-3) as isothermal, determine the net rate of radiative heat loss from the cylinder Q_rad1 using network analysis. What is the temperature of the adiabatic walls T₃? Solve this problem using the radiosity equation.

 

 

 

 

 

 

 

Solution:

The radiosity equations can be written for the 3 surfaces in the illustration:

Surface-1:

Surface-2:

Surface-3:

In matrix form these equations are expressed as:

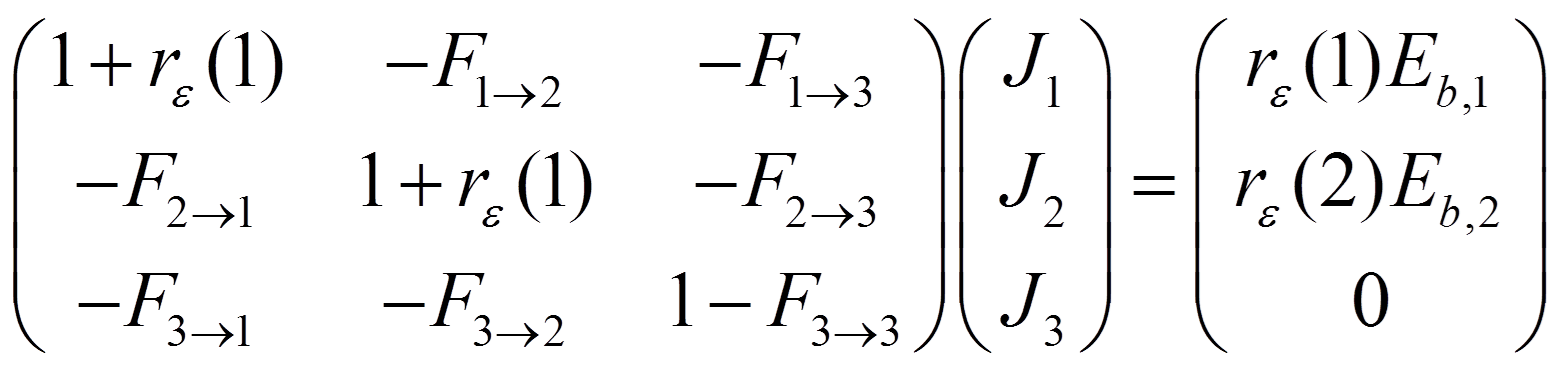
Where .

 

This system of equations is solved as follows:

L=1;

D=L/2;

T1=1000;

T2=500;

e=[0.7; 0.2; 1.];

A=[pi*D*1; L*1; 3*L*1];

 

F=zeros(3,3);

F(1,2)=1/4;               % symmetry

F(1,3)=1-F(1,2);          % summation rule

 

F(2,1)=A(1)*F(1,2)/A(2);  % reciprocity

F(3,1)=A(1)*F(1,3)/A(3);  % reciprocity

 

F(2,3)=1-F(2,1);          % summation rule

F(3,2)=A(2)*F(2,3)/A(3);  % reciprocity

 

F(3,3)=1-F(3,1)-F(3,2);   % summation rule

 

re=e./(1-e);

C=[1+re(1) -F(1,2) -F(1,3); ...

   -F(2,1) 1+re(2) -F(2,3); ...

   -F(3,1) -F(3,2) 1-F(3,3)];

 

D =[re(1)*Eblk(T1); re(2)*Eblk(T2); 0];

J = C\D;

 

The radiative flux of heat from each surface is determined from the radiosity equations:

q=J-F*J; 

Q=q.*A

Q =

   9.6075e+03

  -9.6075e+03

   0.0000e+00

 

Therefore, the net radiative heat loss of heat from the cylinder is Q_rad1=9607.5 W

The temperature T₃=968.9 K is determined from the surface-3 radiosity J₃:

T3=(J(3)/sig).^0.25

T3 =  968.86